Python - Recursion
Đệ quy là một khái niệm lập trình cơ bản, trong đó một hàm gọi chính nó để giải quyết một vấn đề. Kỹ thuật này chia nhỏ một vấn đề phức tạp thành các tiểu vấn đề nhỏ hơn và dễ quản lý hơn cùng loại. Trong Python, đệ quy được thực hiện bằng cách định nghĩa một hàm mà trong thân hàm đó, nó thực hiện một hoặc nhiều cuộc gọi đến chính nó.
Components of Recursion
Như chúng ta đã thảo luận trước đây, đệ quy là một kỹ thuật mà trong đó một hàm gọi chính nó. Để hiểu rõ về đệ quy, cần phải biết các thành phần chính của nó. Dưới đây là các thành phần chính của đệ quy:
- Base Case
- Recursive Case
Base Case
Trường hợp cơ bản là một khái niệm nền tảng trong đệ quy, nếu đóng vai trò là điều kiện mà tại đó một hàm đệ quy ngừng gọi chính nó. Nó rất quan trọng để ngăn chặn đệ quy vô hạn và các lỗi tràn ngăn xếp sau đó.
Trường hợp cơ bản cung cấp một giải pháp trực tiếp cho trường hợp đơn giản nhất của vấn đề, đảm bảo rằng mỗi cuộc gọi đệ quy tiến gần hơn đến điều kiện kết thúc này.
Ví dụ phổ biến nhất về đệ quy là tính giai thừa. Về mặt toán học, giai thừa được định nghĩa là −
n! = n × (n-1)!
Có thể thấy rằng chúng ta sử dụng chính giai thừa để định nghĩa giai thừa. Do đó, đây là một trường hợp phù hợp để viết một hàm đệ quy. Hãy mở rộng định nghĩa trên để tính giá trị giai thừa của 5.
5! = 5 × 4! 5 × 4 × 3! 5 × 4 × 3 × 2! 5 × 4 × 3 × 2 × 1! 5 × 4 × 3 × 2 × 1 = 120
Trong khi chúng ta có thể thực hiện phép tính này bằng cách sử dụng vòng lặp, hàm đệ quy của nó liên quan đến việc gọi liên tiếp nó bằng cách giảm dần số cho đến khi nó đạt đến 1.
Example
Ví dụ sau đây cho thấy cách bạn có thể sử dụng một hàm đệ quy để tính giai thừa −
def factorial(n):
if n == 1:
print (n)
return 1 #base case
else:
print (n,'*', end=' ')
return n * factorial(n-1) #Recursive case
print ('factorial of 5=', factorial(5))
Chương trình trên tạo ra đầu ra sau đây −
5 * 4 * 3 * 2 * 1 factorial of 5= 120
Recursive Case
Trường hợp đệ quy là phần của một hàm đệ quy, nơi hàm gọi chính nó để giải quyết một trường hợp nhỏ hơn hoặc đơn giản hơn của cùng một vấn đề. Cơ chế này cho phép một vấn đề phức tạp được chia nhỏ thành các tiểu vấn đề dễ quản lý hơn, trong đó mỗi tiểu vấn đề là một phiên bản nhỏ hơn của vấn đề gốc.
Trường hợp đệ quy là rất quan trọng để tiến tới trường hợp cơ sở, đảm bảo rằng đệ quy sẽ cuối cùng kết thúc.
Example
Dưới đây là ví dụ về trường hợp đệ quy. Trong ví dụ này, chúng tôi đang tạo ra dãy số Fibonacci, trong đó trường hợp đệ quy cộng tổng các kết quả của hai số Fibonacci trước đó.
def fibonacci(n):
if n <= 0:
return 0 # Base case for n = 0
elif n == 1:
return 1 # Base case for n = 1
else:
return fibonacci(n - 1) + fibonacci(n - 2) # Recursive case
fib_series = [fibonacci(i) for i in range(6)]
print(fib_series)
Chương trình trên tạo ra đầu ra sau đây −
[0, 1, 1, 2, 3, 5]
Binary Search using Recursion
Tìm kiếm nhị phân là một thuật toán mạnh mẽ để nhanh chóng tìm các phần tử trong danh sách đã sắp xếp, với độ phức tạp thời gian logarit giúp nó trở nên rất hiệu quả.
Hãy cùng xem một ví dụ khác để hiểu cách hoạt động của đệ quy. Vấn đề ở đây là kiểm tra xem một số đã cho có mặt trong danh sách hay không.
Trong khi chúng ta có thể thực hiện tìm kiếm tuần tự cho một số nhất định trong danh sách bằng cách sử dụng vòng lặp for và so sánh từng số, tìm kiếm tuần tự không hiệu quả, đặc biệt nếu danh sách quá lớn. Thuật toán tìm kiếm nhị phân kiểm tra xem chỉ số 'high' có lớn hơn chỉ số 'low' hay không. Dựa trên giá trị hiện có tại biến 'mid', hàm sẽ được gọi lại để tìm kiếm phần tử.
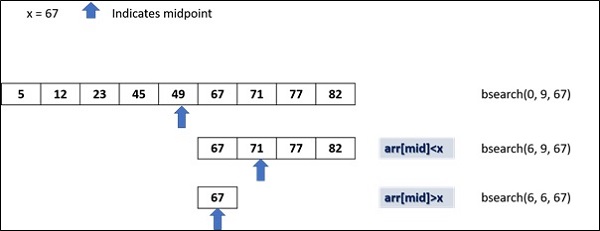
Chúng tôi có một danh sách các số, được sắp xếp theo thứ tự tăng dần. Sau đó, chúng tôi tìm điểm giữa của danh sách và hạn chế việc kiểm tra sang bên trái hoặc bên phải của điểm giữa tùy thuộc vào việc số cần tìm nhỏ hơn hay lớn hơn số tại điểm giữa.
Sơ đồ dưới đây cho thấy cách hoạt động của tìm kiếm nhị phân −
Example
Đoạn mã sau đây triển khai kỹ thuật tìm kiếm nhị phân đệ quy −
def bsearch(my_list, low, high, elem):
if high >= low:
mid = (high + low) // 2
if my_list[mid] == elem:
return mid
elif my_list[mid] > elem:
return bsearch(my_list, low, mid - 1, elem)
else:
return bsearch(my_list, mid + 1, high, elem)
else:
return -1
my_list = [5,12,23, 45, 49, 67, 71, 77, 82]
num = 67
print("The list is")
print(my_list)
print ("Check for number:", num)
my_result = bsearch(my_list,0,len(my_list)-1,num)
if my_result != -1:
print("Element found at index ", str(my_result))
else:
print("Element not found!")
Output
The list is [5, 12, 23, 45, 49, 67, 71, 77, 82] Check for number: 67 Element found at index 5