Python - Set Operators
Set Operators in Python
Các toán tử set trong Python là các ký hiệu và hàm đặc biệt cho phép bạn thực hiện các phép toán khác nhau trên các tập hợp, chẳng hạn như hợp, giao, hiệu và hiệu đối xứng. Các toán tử này cung cấp một cách để kết hợp, so sánh và chỉnh sửa các tập hợp.
Python thực hiện chúng với các toán tử tập hợp sau đây −
Python Set Union Operator (|)
Hợp của hai tập hợp là một tập hợp chứa tất cả các phần tử khác nhau có trong A hoặc trong B hoặc cả hai. Ví dụ,
{1,2}∪{2,3}={1,2,3}
Sơ đồ dưới đây minh họa sự hợp nhất của hai tập hợp.
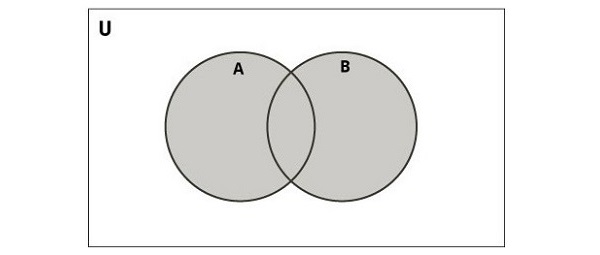
Trong Python, bạn có thể thực hiện phép toán hợp nhất bằng cách sử dụng hàm union() hoặc toán tử | . Phép toán này kết hợp các phần tử của hai tập hợp trong khi loại bỏ các phần tử trùng lặp, dẫn đến một tập hợp mới chứa tất cả các phần tử duy nhất từ cả hai tập hợp.
Example
Ví dụ sau sử dụng toán tử "|" và hàm union(), và trả về hợp của hai tập hợp −
set1 = {1, 2, 3}
set2 = {3, 4, 5}
set3 = {6, 8, 9}
set4 = {9, 45, 73}
union_set1 = set1.union(set2)
union_set2 = set3 | set4
print ('The union of set1 and set2 is', union_set1)
print ('The union of set3 and set4 is', union_set2)
Sau khi thực thi đoạn mã trên, chúng ta nhận được đầu ra sau:
The union of set1 and set2 is {1, 2, 3, 4, 5}
The union of set3 and set4 is {73, 6, 8, 9, 45}
Python Set Intersection Operator (&)
Giao của hai tập hợp AA và BB, được ký hiệu là A∩B, bao gồm tất cả các phần tử chung của cả hai tập hợp A và B. Ví dụ,
{1,2}∩{2,3}={2}
Sơ đồ dưới đây minh họa sự giao nhau của hai tập hợp.
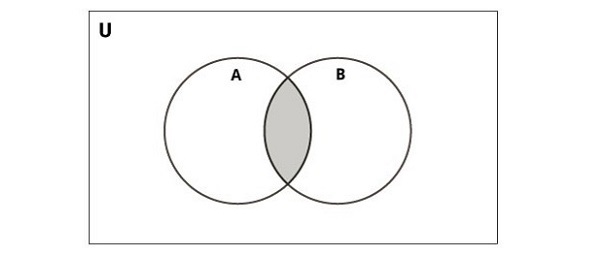
Python cung cấp hàm intersection() hoặc toán tử & để thực hiện thao tác này. Tập hợp kết quả chỉ chứa các phần tử có mặt trong cả hai tập hợp −
Example
Ví dụ sau sử dụng toán tử & và hàm intersection(), và trả về giao của hai tập hợp −
set1 = {1, 2, 3}
set2 = {3, 4, 5}
set3 = {6, 8, 9}
set4 = {9, 8, 73}
intersection_set1 = set1.intersection(set2)
intersection_set2 = set3 & set4
print ('The intersection of set1 and set2 is', intersection_set1)
print ('The intersection of set3 and set4 is', intersection_set2)
Nó sẽ tạo ra đầu ra sau đây −
The intersection of set1 and set2 is {3}
The intersection of set3 and set4 is {8, 9}
Python Set Difference Operator (-)
Sự khác biệt (phép trừ) giữa hai tập hợp bao gồm các phần tử có trong tập hợp đầu tiên nhưng không có trong tập hợp thứ hai. Nó được định nghĩa như sau. Tập hợp A−B bao gồm các phần tử có trong A nhưng không có trong B. Ví dụ,
If A={1,2,3} and B={3,5}, then A−B={1,2}
Sơ đồ dưới đây minh họa sự khác biệt của hai tập hợp −
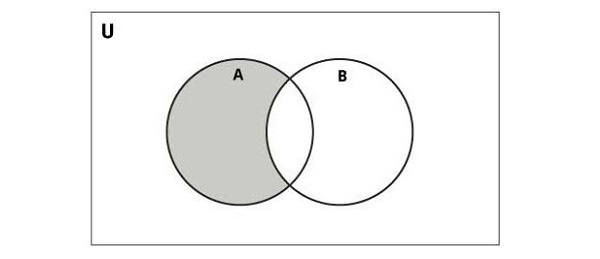
Python cung cấp hàm difference() hoặc toán tử - để thực hiện thao tác này. Tập hợp kết quả chứa các phần tử duy nhất của tập hợp đầu tiên −
Example
Ví dụ sau sử dụng toán tử "-" và hàm difference(), và trả về hiệu của hai tập hợp −
set1 = {1, 2, 3}
set2 = {3, 4, 5}
set3 = {6, 8, 9}
set4 = {9, 8, 73}
difference_set1 = set1.difference(set2)
difference_set2 = set3 - set4
print ('The difference between set1 and set2 is', difference_set1)
print ('The difference between set3 and set4 is', difference_set2)
Chúng ta nhận được đầu ra như được hiển thị bên dưới −
The difference between set1 and set2 is {1, 2}
The difference between set3 and set4 is {6}
Lưu ý rằng "s1-s2" không giống như "s2-s1".
Python Set Symmetric Difference Operator
Sự khác biệt đối xứng của hai tập hợp bao gồm các phần tử có mặt trong một trong hai tập nhưng không có trong cả hai tập. Sự khác biệt đối xứng của A và B được ký hiệu là "A Δ B" và được định nghĩa bởi −
A Δ B = (A − B) ⋃ (B − A)
Nếu A = {1, 2, 3, 4, 5, 6, 7, 8} và B = {1, 3, 5, 6, 7, 8, 9}, thì A Δ B = {2, 4, 9}.
Sơ đồ dưới đây minh họa sự khác biệt đối xứng giữa hai tập hợp −
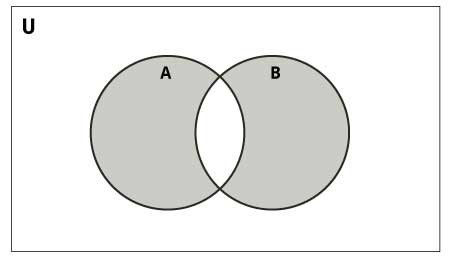
Python cung cấp hàm symmetric_difference() hoặc toán tử ^ để thực hiện thao tác này. Tập hợp kết quả chứa các phần tử độc nhất của mỗi tập hợp.
Example
Ví dụ dưới đây sử dụng toán tử "^" và hàm symmetric_difference(), và trả về sự khác biệt đối xứng của hai tập hợp −
set1 = {1, 2, 3}
set2 = {3, 4, 5}
set3 = {6, 8, 9}
set4 = {9, 8, 73}
symmetric_difference_set1 = set1.symmetric_difference(set2)
symmetric_difference_set2 = set3 ^ set4
print ('The symmetric difference of set1 and set2 is', symmetric_difference_set1)
print ('The symmetric difference of set3 and set4 is', symmetric_difference_set2)
Kết quả thu được như sau −
The symmetric difference of set1 and set2 is {1, 2, 4, 5}
The symmetric difference of set3 and set4 is {73, 6}
Python Subset Testing Operation
Bạn có thể kiểm tra xem một tập hợp có phải là tập con của tập hợp khác hay không bằng cách sử dụng hàm issubset() hoặc toán tử <= . Một tập hợp A được coi là tập con của một tập hợp khác B nếu tất cả các phần tử của A cũng có mặt trong B .
Example
Ví dụ dưới đây sử dụng toán tử "<=" và hàm issubset(), và trả về kết quả kiểm tra tập con của hai tập hợp −
set1 = {1, 2}
set2 = {1, 2, 3, 4}
set3 = {64, 47, 245, 48}
set4 = {64, 47, 3}
is_subset1 = set1.issubset(set2)
is_subset2 = set3 <= set4
print ('set1 is a subset of set2:', is_subset1)
print ('set3 is a subset of set4:', is_subset2)
Kết quả thu được như sau −
set1 is a subset of set2: True set3 is a subset of set4: False